힙(Heap)이란?
힙(Heap)이란 최댓값/최솟값을 빠르게 찾기 위해 고안되었으며, 루트 노드가 언제나 최댓값(최대 힙) 또는 최솟값(최소 힙)을 가지는 완전 이진트리(Complete Binary Tree)이다. 일반적인 리스트를 활용하여 최댓값/최솟값을 찾기 위한 max()/min() 함수의 시간 복잡도는 O(n)이다. 그러나 힙을 사용하면 O(log n)으로 수행이 가능하며, 정렬도 O(n log n)의 빠른 속도로 가능하다.
연산에 대한 자세한 이해보다는 힙에 대한 개념과 파이썬에서 활용할 수 있는 방법을 이해하는 것을 목표로 한다.
완전 이진 트리(Complete Binary Tree)
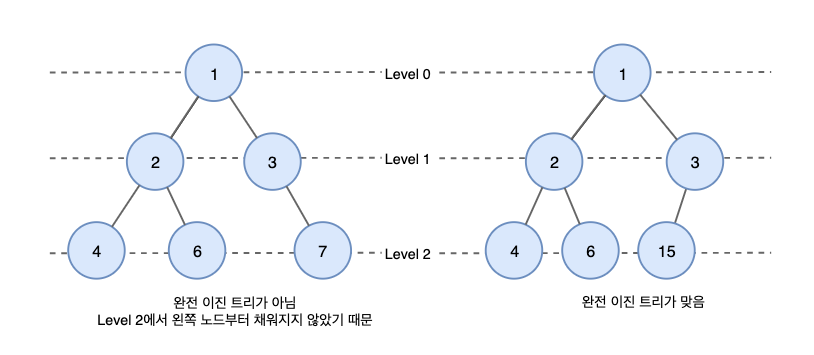
마지막 레벨(Level)을 제외한 모든 레벨은 완전히 채워져 있는 이진트리이다. 삽입 연산을 수행할 경우 마지막 레벨의 가장 왼쪽부터 채워지며, 해당 레벨이 가득 찰 경우 다음 레벨로 넘어간다.
최대 힙(Max Heap) vs 최소 힙(Min Heap)
힙은 최대 힙과 최소 힙으로 나뉜다. 최대힙은 자식 노드보다 부모의 노드의 값이 크고, 최소 힙은 자식 노드보다 부모의 노드의 값이 더 작다. 힙을 구성하는 규칙은 부모-자식 간의 크기 밖에 없기 때문에 이진 탐색 트리(Binary Search Tree)에 비해 부드럽게(?) 구성된다. 예를 들어 아래 사진의 최대 힙에서 10과 8의 위치가 바뀌어도 최대 힙의 규칙에 어긋나지 않지만, 이진 탐색 트리의 경우 정해진 위치가 존재한다.

힙 연산
힙에는 크게 두 가지 삽입/삭제 연산이 존재한다. 해당 연산들은 모두 O(log n)으로 수행이 가능하다. 아래의 최대 힙 구조의 트리를 기준으로 두 개의 연산이 어떻게 이루어지는지 살펴보자.

삽입
완전 이진 트리에 삽입하는 것이므로 마지막 레벨의 가장 왼쪽에 삽입이 진행된다. 그리고 부모 노드와 값을 비교하여 삽입된 값이 더 크다면 자리를 바꾼다. 부모 노드의 값이 크거나 같을 때까지 해당 작업을 반복한다.
위의 이진 트리에 9라는 새로운 노드를 삽입한다고 해보자. 완전 이진 트리에 삽입하는 것이므로 마지막 레벨, 가장 왼쪽에 삽입한다.

삽입된 노드(9)와 부모 노드(8)과 비교하면, 삽입된 노드가 더 크기 때문에 부모 노드와 자리를 바꾼다. 다음으로 부모 노드(15)와 비교하면, 부모 노드의 값이 더 크기에 삽입 연산은 끝나게 된다.

삭제
최댓값을 가지는 루트 노드를 삭제하고, 마지막 노드를 루트 노드로 옮긴다. 이후 자식 노드와 값을 비교하여 더 큰 값과 자리를 바꾼다. 만약 자신이 가장 클 경우 삭제 연산은 끝나게 된다.
위의 이진 트리에서 삭제 연산을 진행한다고 해보자. 먼저 최댓값을 지닌 루트 노드의 값을 삭제한다.

이후 마지막 노드를 루트 노드에 복사하고, 자식 노드(10, 8)와 값을 비교하여 더 큰 값을 지닌 자식 노드인 10과 자리를 바꾼다.

자식 노드(3)와 비교했을 때, 자신이 더 크므로 삭제 연산은 끝나게 된다.

Python에서의 힙 사용
파이썬의 heapq 라이브러리를 사용해서 힙 연산을 수행할 수 있다.
import heapq힙 연산
heapq 라이브러리에는 다양한 함수가 존재하지만, heapify(), heappush(), heappop() 3개의 함수만 소개하려고 한다. 다른 함수도 공부해보고 싶다면, 참고링크의 'Python 공식 문서'를 참고하면 된다.
heapify(x)
리스트 x를 선형 시간 즉, O(n)으로 힙으로 변환한다. heappush()를 사용해 변환하면 O(n log n)인데, 가능하다면 heapify()를 사용하는 게 효율적이다. 기본적으로 최소 힙으로 구성하며 최대 힙을 따로 제공하지 않는다.
l = [16, 2, 5, 10, 30, 20]
heapq.heapify(l)
l
# result : [2, 10, 5, 16, 30, 20]heappush(heap, item)
최소 힙을 유지하면서, item 값을 힙에 push한다.
l = [16, 2, 5, 10, 30, 20]
heapq.heapify(l)
heapq.heappush(l, 6)
l
# result : [2, 10, 5, 16, 30, 20, 6]heappop(heap)
최소 힙을 유지하면서 heap에서 가장 작은 항목(루트 노드)을 제거 및 반환한다. 힙이 비어 있으면 IndexError가 발생한다. 만약 힙에서 제거하지 않고 최솟값만 반환하고 싶다면, [list[0]]과 같은 형태를 인자로 넣어주면 된다.
l = [16, 2, 5, 10, 30, 20]
heapq.heapify(l)
heapq.heappop(l)
l
# result : [5, 10, 20, 16, 30]힙 구성
최소 힙 구성
heapify(list) 또는 heappush(heap, item)를 사용해서 리스트를 힙으로 변환할 수 있다. 시간 복잡도는 각각 O(n), O(n log n)이며, 똑같이 리스트의 형태를 한 상태에서 순서가 바뀐 모습을 확인할 수 있다.
l = [16, 2, 5, 10, 30, 20]
heapq.heapify(l)
l
# result : [2, 10, 5, 16, 30, 20]l = [16, 2, 5, 10, 30, 20]
heap = []
for v in l:
heapq.heappush(heap, v)
l
# result : [2, 10, 5, 16, 30, 20]최대 힙 구성
최대 힙을 구성하기 위해서는 추가적인 작업이 필요하다. 리스트의 부호를 음수로 하여 push 하고, 다시 부호를 바꿔주면 최대 힙으로 구성할 수 있다. 그러나 heappop은 최소 힙을 기준으로 진행되기에 최대 힙 상태에서 heappop을 진행할 경우 올바르게 동작하지 않는다.
l = [16, 2, 5, 10, 30, 20]
heap = []
for v in l:
heapq.heappush(heap, -v)
for i in range(len(heap)):
heap[i] *= -1
heap
# result : [30, 20, 10, 5, 16]힙 정렬
최소 힙 정렬
최소 힙으로 구성된 리스트에 heappop()을 길이만큼 수행하면, 오름차순으로 정렬된 출력 결과를 얻을 수 있다. 이를 다른 리스트에 저장하여 재정렬하면 내림차순의 결과도 얻을 수 있을 것이다.
l = [16, 2, 5, 10, 30, 20]
heapq.heapify(l)
for i in range(len(l)):
print(heapq.heappop(l), end = " ")
# result : 2 5 10 16 20 30최대 힙 정렬
음수를 취하여 최대 힙의 형태로 변환해 준 뒤 다시 음수를 취하여 출력하면 내림차순으로 정렬된 결과를 얻을 수 있다.
l = [16, 2, 5, 10, 30, 20]
heap = []
for v in l:
heapq.heappush(heap, -v)
for i in range(len(heap)):
print(heapq.heappop(heap) * -1, end=" ")
# result : 30 20 16 10 5 2참고링크
Python 공식 문서 : heapq
https://docs.python.org/ko/3/library/heapq.html
[자료구조] 힙(Heap) 이해하기
https://velog.io/@gnwjd309/data-structure-heap
[자료구조] 이진 트리 (Binary Tree) 알아보기
https://yoongrammer.tistory.com/69
[Python] 힙 자료구조인 heapq에 대해 알아보자!
https://www.jongung.com/290#%EC%B5%9C%EB%8C%80%20%ED%9E%99%20%EA%B5%AC%ED%98%84-1
