문제
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
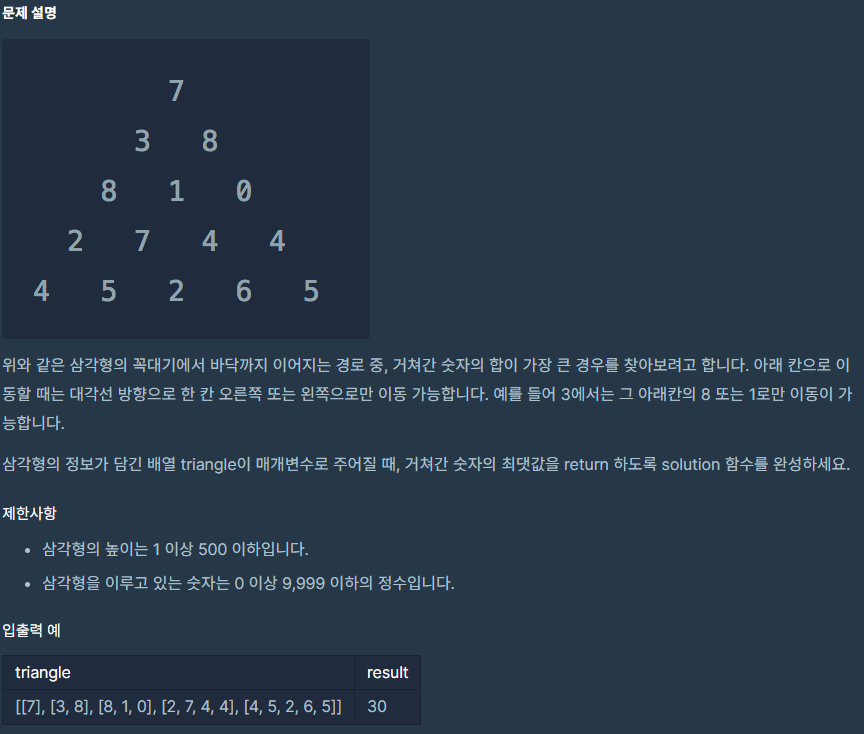
문제 이해
- 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾음
- 아래로 이동할 때는 대각선 오른쪽/왼쪽 한 칸으로만 이동 가능
- 배열 triangle이 주어질 때, 최댓값을 반환하도록 작성
풀이 (1)
배열 triangle을 len(triangle) - 2(마지막에서 한 칸 위)부터 역으로 순회하여 수를 더함
대각선 한 칸 아래 오른쪽/왼쪽 중에 더했을 때, 더 큰 값을 해당 칸에 대입
코드
문제에 제공된 예로 순서를 설명하면, [2, 7, 4, 4]가 나타난 행부터 순회를 시작한다. 그리고 2+4, 2+5 중에 큰 값을 해당 칸에 대입한다. 즉 2([3][0])에 7을 대입한다. 이후 7+5, 5+2 중 큰 12를 7에 대입한다. 이러한 방식으로 진행하면, 아래에서 위로 진행하며, 최댓값을 계속해서 더해온 triangle[0][0]에는 최종적인 최댓값이 저장될 것이다.
def solution(triangle):
for i in range(len(triangle) - 2, -1, -1):
for j in range(len(triangle[i])):
triangle[i][j] = max(triangle[i+1][j] + triangle[i][j], triangle[i+1][j+1] + triangle[i][j])
return triangle[0][0]
풀이 (2)
배열 triangle을 두 번째 행부터 순회하여 수를 더함
합을 저장할 dp 배열을 활용 및 배열 triangle을 순회하며, 위의 수와 더했을 때 큰 값을 해당 칸에 대입
코드
문제에 제공된 예로 순서를 설명하면, [3, 8]이 나타난 행부터 순회를 진행한다. 1행에는 숫자가 하나 밖에 없으므로 [10, 15]로 변경될 것이다. 이후 다음 행을 진행하며, [10+8, max(10+1, 15+1), 15+0]이 될 것이다. 이러한 방식으로 진행하면, 결국 마지막 행 중 하나의 원소가 최댓값이 된다. 그러나 해당 행의 첫 번째 원소의 경우 대각선 위 왼쪽이 존재하지 않으므로 예외 처리를 해주어야 하고, 마지막 원소의 경우에는 dp 초기화 시 0으로 진행하기 때문에 따로 예외 처리해주지 않아도 +0이 되어 정상적으로 작동한다.
효율성 테스트의 경우 풀이 (1)이 더 빠른 것을 확인할 수 있다. 풀이 (2)의 경우 배열 dp를 초기화를 진행하고, 배열 triangle의 모든 원소 - 1 만큼 순회하므로 당연히 추가 자원이 없고 모든 원소 - (마지막 행 원소 수) 만큼 순회하므로 풀이 (1)보다는 느리다.
def solution(triangle):
h = len(triangle)
dp = [[0 for i in range(h)] for j in range(h)]
dp[0][0] = triangle[0][0]
for i in range(1, h):
for j in range(len(triangle[i])):
if j == 0:
dp[i][j] = dp[i-1][j] + triangle[i][j]
else:
dp[i][j] = max(dp[i-1][j-1] + triangle[i][j], dp[i-1][j] + triangle[i][j])
return max(dp[h-1])
'알고리즘 연습 > 프로그래머스' 카테고리의 다른 글
| [Python - Lv.3] 이중우선순위큐 (0) | 2024.04.02 |
|---|---|
| [Python - Lv.2] 행렬의 곱셈 (0) | 2024.03.23 |
| [Python - Lv.2] 전화번호 목록 (0) | 2024.03.21 |
| [Python - Lv.2] 프로세스 (0) | 2024.03.20 |
| [Python - Lv.2] 의상 (0) | 2024.03.19 |
