이산 확률 분포
모든 확률 분포는 연속 확률 분포 또는 이산 확률 분포로 분류할 수 있다. 만약 변수가 두 값 사이의 어떤 값이든 가질 수 있으면 연속 변수라고 하고, 그렇지 않으면 이산 변수라고 한다. 확률 변수가 이산적일 경우, 그 확률 분포를 이산 확률 분포라고 말한다.
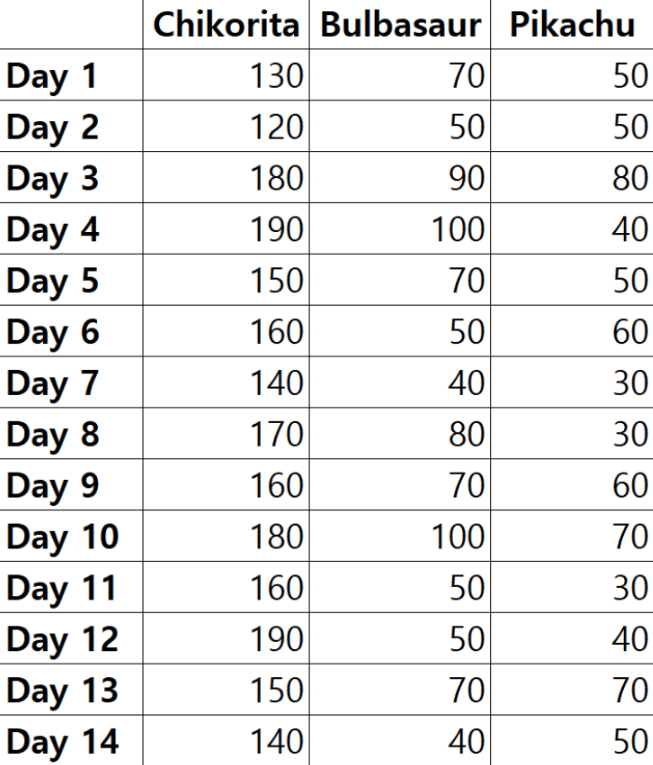
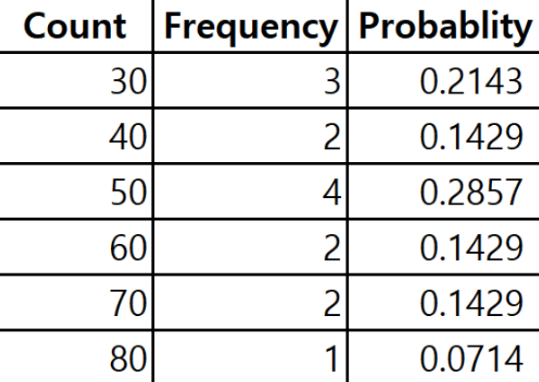
기댓값 함수
기댓값 함수를 사용해서 하루 평균 몇 마리의 피카츄를 잡을 수 있는지 계산할 수 있다. 각 xi에 피카츄를 잡을 수 있을 것으로 기대하는 확률 p + i를 곱해주고, 그 값들을 모두 더한다.
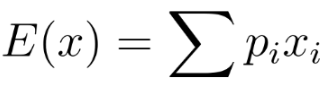
E(x) = 0.2143*30 + 0.1429*40 + 0.2857*50 + 0.1429*60 + 0.1429*70 + 0.0714*80 = 50.719
평균적으로 하루에 51마리의 피카츄를 잡을 것으로 기대된다는 것이며, 동시에 데이터 셋의 평균을 의미한다.
분산과 표준 편차
분산은 데이터 셋이 퍼져 있는 정도를 측정하는 하나의 방법이며, 평균으로부터 편차의 제곱합으로 정의된다. 이산 확률 분포에서 분산은 다음 식으로 계산된다.
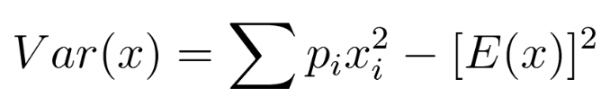
Var(x) = 0.2143*30^2 +0.1429*40^2 +0.2857*50^2 + 0.1429*60^2 + 0.1429*70^2 + 0.0714*80^2 – 50.719^2 = 234.953039
표준편차는 간단히 분산의 제곱근과 같다.
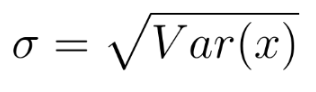
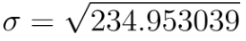
= 15.32817794
유명한 이산 확률 분포
- 베르누이 분포
- 이항 분포
- 다항 분포
- 초기하 분포
- 음 이항 분포
- 푸아송 분포
- 기하 분포
- 이산 균등 분포
- 적률 생성
베르누이 분포
베르누이 분포는 베르누이 시행을 여러 번 했을 경우의 확률 분포이다. 베르누이 시행의 한 예로는 동전 던지기가 있다. 두 가지 경우의 값, 주로 0과 1만 가질 수 있는 이산 확률 분포의 가장 쉬운 예이다. 중요한 것은 측정하는 변수가 확률 변수이면서 독립이어야 한다. 이는 매 시행마다 확률이 같다는 의미이며, 확률이 변한다면 베르누이 분포는 정확하지 않을 수 있다.
베르누이 시행의 성공 확률은 P로 정의되고, 실패 확률은 1 - P이다. 연속한 베르누이 시행의 분산은 데이터 셋의 값들이 얼마나 퍼져있는지를 측정하는 척도이다.
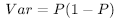
푸아송 분포
특정 간격 동안 발생한 사건의 확률을 계산할 때 사용한다. 간격은 시간, 면적, 부피 또는 거리 중 하나일 수 있다. 가능한 사건의 경우가 많고 각각의 확률이 낮을 때 주로 사용한다. 평균과 분산은 lamda로 같다.
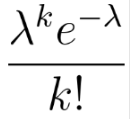
k = 0, 1, 2, 3, ... (각 사건의 성공 횟수)
e = (오일러 상수)
lamda = 주어진 시간 동안 공간 간격에서의 성공 횟수
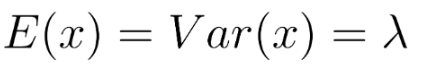
푸아송 분포의 두 가지 조건
- 각 성공 사건은 독립이어야 한다.
- 짧은 간격 동안 성공할 확률과 긴 간격 동안 성공할 확률은 동일해야 한다.
적용 사례
- 프로이센 군대에서 말이 발을 차서 죽는 사람의 수
- 선천적 결함과 유전적 돌연변이
- 희귀병
- 차 사고
- 교통 흐름과 이상적인 앞뒤 차의 간격
- 한 페이지에 있는 오타 수
- 일 년에 지구에 부딪히는 직경 1 미터 이상의 운석의 수
참고 링크
DataLit : 데이터 다루기
'프로젝트 단위 공부 > [부스트코스] DataLit : 데이터 다루기' 카테고리의 다른 글
| Ch1-9. 데이터 시각화하기 (0) | 2023.07.21 |
|---|---|
| Ch1-7. 확률 변수 (0) | 2023.07.20 |
| Ch1-3. 텍스트 데이터 정제 (0) | 2023.07.17 |
| Ch1-2. SQL 테크닉 (0) | 2023.07.17 |
| Ch1-1. 파이썬 정규표현식 다시보기 (0) | 2023.07.17 |
이산 확률 분포
모든 확률 분포는 연속 확률 분포 또는 이산 확률 분포로 분류할 수 있다. 만약 변수가 두 값 사이의 어떤 값이든 가질 수 있으면 연속 변수라고 하고, 그렇지 않으면 이산 변수라고 한다. 확률 변수가 이산적일 경우, 그 확률 분포를 이산 확률 분포라고 말한다.


기댓값 함수
기댓값 함수를 사용해서 하루 평균 몇 마리의 피카츄를 잡을 수 있는지 계산할 수 있다. 각 xi에 피카츄를 잡을 수 있을 것으로 기대하는 확률 p + i를 곱해주고, 그 값들을 모두 더한다.
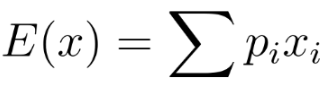
E(x) = 0.2143*30 + 0.1429*40 + 0.2857*50 + 0.1429*60 + 0.1429*70 + 0.0714*80 = 50.719
평균적으로 하루에 51마리의 피카츄를 잡을 것으로 기대된다는 것이며, 동시에 데이터 셋의 평균을 의미한다.
분산과 표준 편차
분산은 데이터 셋이 퍼져 있는 정도를 측정하는 하나의 방법이며, 평균으로부터 편차의 제곱합으로 정의된다. 이산 확률 분포에서 분산은 다음 식으로 계산된다.
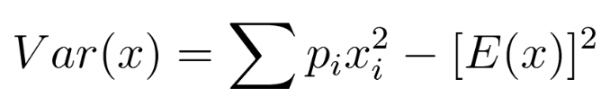
Var(x) = 0.2143*30^2 +0.1429*40^2 +0.2857*50^2 + 0.1429*60^2 + 0.1429*70^2 + 0.0714*80^2 – 50.719^2 = 234.953039
표준편차는 간단히 분산의 제곱근과 같다.
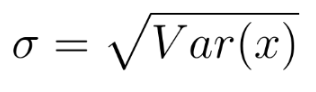
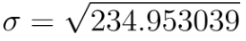
= 15.32817794
유명한 이산 확률 분포
- 베르누이 분포
- 이항 분포
- 다항 분포
- 초기하 분포
- 음 이항 분포
- 푸아송 분포
- 기하 분포
- 이산 균등 분포
- 적률 생성
베르누이 분포
베르누이 분포는 베르누이 시행을 여러 번 했을 경우의 확률 분포이다. 베르누이 시행의 한 예로는 동전 던지기가 있다. 두 가지 경우의 값, 주로 0과 1만 가질 수 있는 이산 확률 분포의 가장 쉬운 예이다. 중요한 것은 측정하는 변수가 확률 변수이면서 독립이어야 한다. 이는 매 시행마다 확률이 같다는 의미이며, 확률이 변한다면 베르누이 분포는 정확하지 않을 수 있다.
베르누이 시행의 성공 확률은 P로 정의되고, 실패 확률은 1 - P이다. 연속한 베르누이 시행의 분산은 데이터 셋의 값들이 얼마나 퍼져있는지를 측정하는 척도이다.
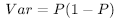
푸아송 분포
특정 간격 동안 발생한 사건의 확률을 계산할 때 사용한다. 간격은 시간, 면적, 부피 또는 거리 중 하나일 수 있다. 가능한 사건의 경우가 많고 각각의 확률이 낮을 때 주로 사용한다. 평균과 분산은 lamda로 같다.
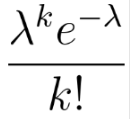
k = 0, 1, 2, 3, ... (각 사건의 성공 횟수)
e = (오일러 상수)
lamda = 주어진 시간 동안 공간 간격에서의 성공 횟수
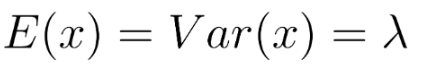
푸아송 분포의 두 가지 조건
- 각 성공 사건은 독립이어야 한다.
- 짧은 간격 동안 성공할 확률과 긴 간격 동안 성공할 확률은 동일해야 한다.
적용 사례
- 프로이센 군대에서 말이 발을 차서 죽는 사람의 수
- 선천적 결함과 유전적 돌연변이
- 희귀병
- 차 사고
- 교통 흐름과 이상적인 앞뒤 차의 간격
- 한 페이지에 있는 오타 수
- 일 년에 지구에 부딪히는 직경 1 미터 이상의 운석의 수
참고 링크
DataLit : 데이터 다루기
'프로젝트 단위 공부 > [부스트코스] DataLit : 데이터 다루기' 카테고리의 다른 글
| Ch1-9. 데이터 시각화하기 (0) | 2023.07.21 |
|---|---|
| Ch1-7. 확률 변수 (0) | 2023.07.20 |
| Ch1-3. 텍스트 데이터 정제 (0) | 2023.07.17 |
| Ch1-2. SQL 테크닉 (0) | 2023.07.17 |
| Ch1-1. 파이썬 정규표현식 다시보기 (0) | 2023.07.17 |
