확률 변수
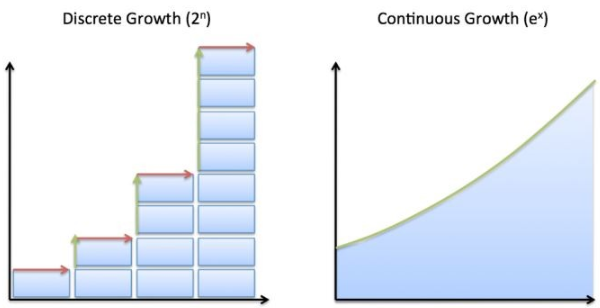
확률과 통계학에서 확률 변수(random variable)는 모두 가능한 값이 랜덤 현상의 결과인 변수를 말한다. 확률 변수는 이산적이거나 연속적인데, 이산적이라는 의미는 확률 변수의 확률 분포가 확률 질량 함수 특성을 가지고 있어 유한 개 혹은 셀 수 있는 수의 들 중에서 하나를 취할 수 있다는 뜻이다. 연속적이라는 의미는 확률 변수의 확률 분포가 확률 밀도 함수 특성을 가지고 있어 구간이나 구간 집합에서 임의의 값을 취할 수 있다는 뜻이다.
이산 확률 분포
확률 변수는 예측할 수 없는 확률 과정의 결과를 수량, 특히 실수와 매핑하는 함수로 정의한다. 확률 변수는 함수의 입력값으로 들어가는 기저 확률 과정의 결과에 의존한다는 점에서(특히, 종속 변수)이며, 기저 확률 과정이 확률적이라는 점에서 확률성을 가진다.
이산 확률 변수의 예
- 가족 중 자녀의 수
- 금요일 밤의 영화관 출입
- 의사가 수술한 환자의 수
- 전구 10개 들이 박스 중 불량품의 수
이산 확률 변수의 확률 분포는 각 가능한 값들에 대한 확률들의 목록이다. 확률 함수 혹은 확률 질량 함수라고 부른다.
연속 확률 분포
연속 확률 변수는 특정한 값들의 집합에서 정의되지 않는다. 대신 값들의 구간 위에서 정의되며, 우측 그림에서 곡선 아래 면적으로 표현된다. 확률 변수가 가질 수 있는 값의 수가 무한이기 때문에 임의의 한 값을 측정할 확률은 0이다.
확률 변수 X가 실수 전체에 걸쳐 모든 값을 가질 수 있다고 가정하였다. 그럼 X가 결과의 집합 A에 속할 확률은 P(A)이며, A안에 있고 곡성 아래에 있는 영역ㅇ로 정의된다. 곡선은 밀도 곡선이라 부르며, 함수 p(x)라고 표현한다.
p(x)가 만족하는 조건
- 곡선은 음의 값을 갖지 않는다. 모든 x에 대하여 p(x) > 0
- 곡선 아래 모든 영역의 넓이는 1이다.
연속 확률 변수의 예
- 키
- 무게
- 오렌지에 있는 과당의 양
- 1마일 뛰는 데 걸리는 시간
한 가지 예를 살펴보자. 한 실험에서 무작위로 선택된 사람의 키를 확률 변수라고 한다. 수학적으로 확률 변수는 사람과 그 사람의 키를 매핑하는 함수를 뜻한다. 확률 변수에 대한 확률 분포를 통해 키가 어떤 부분집합에 속할 확률을 계산할 수 있다. 예를 들면, 180cm 이상 190cm 이하에 속할 확률을 계산할 수 있다.
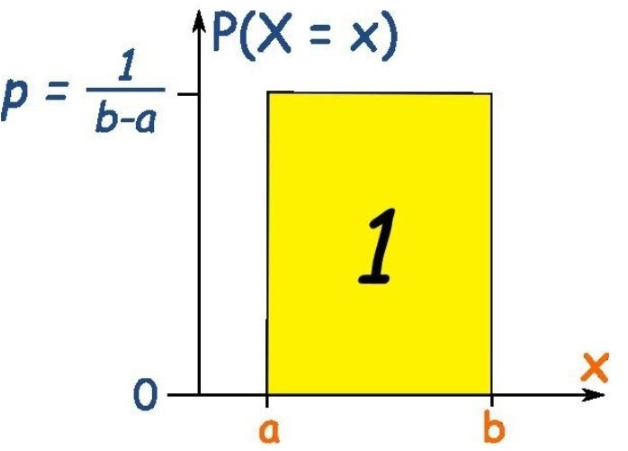
균등 분포
a와 b 사이의 모든 확률 변수들에 대해 같은 확률을 갖고 있다.
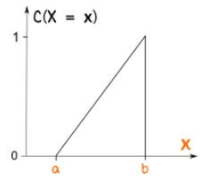
누적 균등 분포(CDF)
균등 분포를 누적(계속 더하여 나가는 것) 분포로 나타낼 수 있다. 확률은 0에서 시작해서 1에서 끝난다.
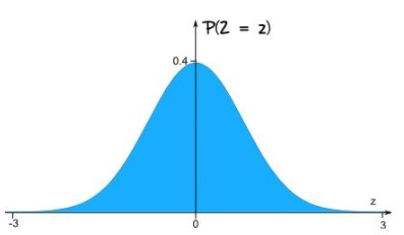
정규 분포
가장 중요한 그래프는 정규 분포이다. 확률 변수는 특별한 문자인 Z로 나타낸다. Z의 그래프는 대칭 종 모양 곡선이다.
참고 링크
DataLit : 데이터 다루기
'프로젝트 단위 공부 > [부스트코스] DataLit : 데이터 다루기' 카테고리의 다른 글
| Ch1-11. 차원 축소 (0) | 2023.07.24 |
|---|---|
| Ch1-9. 데이터 시각화하기 (0) | 2023.07.21 |
| Ch1-6. 이산 확률 (0) | 2023.07.20 |
| Ch1-3. 텍스트 데이터 정제 (0) | 2023.07.17 |
| Ch1-2. SQL 테크닉 (0) | 2023.07.17 |