차원 축소
최근 데이터가 급격히 증가하면서 수많은 변수/차원을 얻게 되었다. 이는 원치 않은 차원 증가 문제이고, 차원 축소 처리가 필요하다. 변수가 많을수록 더 많은 문제가 일어날 수 있다. 이러한 문제를 해결하기 위해 차원 축소 기법이 등장하였다.
통계학, 머신러닝, 정보 이론에서 차원 축소란 주성분 집합을 구해서 확률 변수의 개수를 줄이는 과정을 의미한다. 차원 축소는 특징 선택과 특칭 추출 단계로 나뉜다.
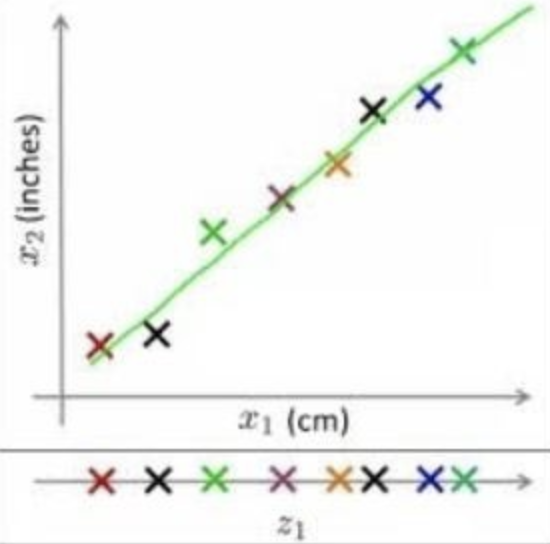
위 그림은 2차원 데이터 x1, x2를 어떤 물체를 센티미터 단위로 측정한 값과 인치 단위로 축정한 값이라고 하자. 기계학습에서 두 차원을 모두 사용하면 비슷한 정보를 전달하게 되고, 시스템에 많은 노이즈를 일으킨다. 따라서 하나의 차원만 사용하는 것이 적절하다.
이처럼 n 차원의 데이터를 k (k<n) 차원 데이터로 축소할 수 있다. 이때 k 차원은 n 차원 벡터 중에서 바로 고를 수도 있고(필터링), 차원의 조합(가중 평균)일 수도 있고, 또 기존의 여러 차원을 잘 나타낼 수 있는 새로운 차원일 수 있다.
차원 축소 방법
- 주성분 분석(PCA): 데이터 간의 전역적인 거리 정보를 보존하는 간단한 선형 방법
- 다차원척도법(MDS): 데이터 간의 전역적인 거리 정보를 보존하는 방법
- 새몬 매핑: MDS의 변형으로 근거리에 더 집중하는 방법
- 데이터 매니폴드의 등척 매핑(ISOMAP): 그래프 기반의 방법(MDS 방법에서 기원)
- 곡선성분분석(CCA): MDS기법을 따르며, 작은 지역의 이웃 데이터 간의 거리를 보존하는 방법
- 최대 분산 전개: 근거리가 보존죈다는 제약 아래에서 분산을 최대화 하는 방법
- 자기조직화지도(SOM): 모든 데이터를 통과하는 표면을 찾는 유연하고 확장성 있는 방법
자기조직화지도(SOM)
자기조직화지도(SOM) 또는 코호넨 네트워크는 튜보 코호넨이 개발하였으며, 데이터 가시화 기술을 제공한다. 데이터 차원을 축소 매핑하여 고차원 데이터를 이해할 수 있도록 돕는다. SOM은 데이터 차원을 축소하고 데이터 간의 유사도를 표시한다.
SOM을 이용한 군집화는 여러 개의 유닛이 현재 객체에 대해 경쟁하도록 하는 방식이다. 데이터가 시스템에 들어가면 인공신경망이 입력에 대한 정보를 얻어 학습한다. 유닛의 가중치가 현재 객체와 가장 비슷한 유닛이 승자/활성 유닛이 된다. 학습 단계에서 입력 변수에 대한 값들이 입력 데이터셋 내 이웃 데이터와의 관계를 보존하면서 점진적으로 조정된다. 입력된 객체와 값이 바뀌면 승자 유닛의 가중치와 그 이웃의 가중치 역시 조정된다.
알고리즘
- 1. 각 노드의 가중치를 초기화한다.
- 2. 학습 데이터 집합에서 무작위로 벡터 하나를 고른다.
- 3. 각 노드의 가중치 중 무엇이 입력 벡터와 가장 가까운지 확인한다. 승자 노드는 Best Matching Unit(BMU)라 부른다.
- 4. BMU의 이웃을 계산한다. 각 이웃의 개수는 시간이 지날수록 줄어든다.
- 5. 승자 노드의 가중치는 표본 벡터와 가까워지도록 바뀐다. 승자의 이웃 노드 역시 표본 벡터와 가까워진다. BMU와 가까운 노드일수록 가중치가 바뀔 가능성이 높고 멀수록 덜 학습된다.
- 6. 2~5를 N번 반복한다.
참고 링크
DataLit : 데이터 다루기
'프로젝트 단위 공부 > [부스트코스] DataLit : 데이터 다루기' 카테고리의 다른 글
| Ch1-과제. 데이터 시각화 (0) | 2023.07.30 |
|---|---|
| Ch1-12. 데이터 시각화 도구 (0) | 2023.07.24 |
| Ch1-9. 데이터 시각화하기 (0) | 2023.07.21 |
| Ch1-7. 확률 변수 (0) | 2023.07.20 |
| Ch1-6. 이산 확률 (0) | 2023.07.20 |
차원 축소
최근 데이터가 급격히 증가하면서 수많은 변수/차원을 얻게 되었다. 이는 원치 않은 차원 증가 문제이고, 차원 축소 처리가 필요하다. 변수가 많을수록 더 많은 문제가 일어날 수 있다. 이러한 문제를 해결하기 위해 차원 축소 기법이 등장하였다.
통계학, 머신러닝, 정보 이론에서 차원 축소란 주성분 집합을 구해서 확률 변수의 개수를 줄이는 과정을 의미한다. 차원 축소는 특징 선택과 특칭 추출 단계로 나뉜다.

위 그림은 2차원 데이터 x1, x2를 어떤 물체를 센티미터 단위로 측정한 값과 인치 단위로 축정한 값이라고 하자. 기계학습에서 두 차원을 모두 사용하면 비슷한 정보를 전달하게 되고, 시스템에 많은 노이즈를 일으킨다. 따라서 하나의 차원만 사용하는 것이 적절하다.
이처럼 n 차원의 데이터를 k (k<n) 차원 데이터로 축소할 수 있다. 이때 k 차원은 n 차원 벡터 중에서 바로 고를 수도 있고(필터링), 차원의 조합(가중 평균)일 수도 있고, 또 기존의 여러 차원을 잘 나타낼 수 있는 새로운 차원일 수 있다.
차원 축소 방법
- 주성분 분석(PCA): 데이터 간의 전역적인 거리 정보를 보존하는 간단한 선형 방법
- 다차원척도법(MDS): 데이터 간의 전역적인 거리 정보를 보존하는 방법
- 새몬 매핑: MDS의 변형으로 근거리에 더 집중하는 방법
- 데이터 매니폴드의 등척 매핑(ISOMAP): 그래프 기반의 방법(MDS 방법에서 기원)
- 곡선성분분석(CCA): MDS기법을 따르며, 작은 지역의 이웃 데이터 간의 거리를 보존하는 방법
- 최대 분산 전개: 근거리가 보존죈다는 제약 아래에서 분산을 최대화 하는 방법
- 자기조직화지도(SOM): 모든 데이터를 통과하는 표면을 찾는 유연하고 확장성 있는 방법
자기조직화지도(SOM)
자기조직화지도(SOM) 또는 코호넨 네트워크는 튜보 코호넨이 개발하였으며, 데이터 가시화 기술을 제공한다. 데이터 차원을 축소 매핑하여 고차원 데이터를 이해할 수 있도록 돕는다. SOM은 데이터 차원을 축소하고 데이터 간의 유사도를 표시한다.
SOM을 이용한 군집화는 여러 개의 유닛이 현재 객체에 대해 경쟁하도록 하는 방식이다. 데이터가 시스템에 들어가면 인공신경망이 입력에 대한 정보를 얻어 학습한다. 유닛의 가중치가 현재 객체와 가장 비슷한 유닛이 승자/활성 유닛이 된다. 학습 단계에서 입력 변수에 대한 값들이 입력 데이터셋 내 이웃 데이터와의 관계를 보존하면서 점진적으로 조정된다. 입력된 객체와 값이 바뀌면 승자 유닛의 가중치와 그 이웃의 가중치 역시 조정된다.
알고리즘
- 1. 각 노드의 가중치를 초기화한다.
- 2. 학습 데이터 집합에서 무작위로 벡터 하나를 고른다.
- 3. 각 노드의 가중치 중 무엇이 입력 벡터와 가장 가까운지 확인한다. 승자 노드는 Best Matching Unit(BMU)라 부른다.
- 4. BMU의 이웃을 계산한다. 각 이웃의 개수는 시간이 지날수록 줄어든다.
- 5. 승자 노드의 가중치는 표본 벡터와 가까워지도록 바뀐다. 승자의 이웃 노드 역시 표본 벡터와 가까워진다. BMU와 가까운 노드일수록 가중치가 바뀔 가능성이 높고 멀수록 덜 학습된다.
- 6. 2~5를 N번 반복한다.
참고 링크
DataLit : 데이터 다루기
'프로젝트 단위 공부 > [부스트코스] DataLit : 데이터 다루기' 카테고리의 다른 글
| Ch1-과제. 데이터 시각화 (0) | 2023.07.30 |
|---|---|
| Ch1-12. 데이터 시각화 도구 (0) | 2023.07.24 |
| Ch1-9. 데이터 시각화하기 (0) | 2023.07.21 |
| Ch1-7. 확률 변수 (0) | 2023.07.20 |
| Ch1-6. 이산 확률 (0) | 2023.07.20 |
